Parallel C++ example problems

ark_heat2D

ARKODE provides one parallel C++ example problem, that extends our previous ark_heat1D test to now simulate a two-dimensional heat equation,

\[\frac{\partial u}{\partial t} = k_x \frac{\partial^2 u}{\partial x^2} + k_y \frac{\partial^2 u}{\partial y^2} + h,\]

for \(t \in [0, 0.3]\), and \((x,y) \in [0, 1]^2\), with initial condition \(u(0,x,y) = 0\), stationary boundary conditions,

\[\frac{\partial u}{\partial t}(t,0,y) = \frac{\partial u}{\partial t}(t,1,y) = \frac{\partial u}{\partial t}(t,x,0) = \frac{\partial u}{\partial t}(t,x,1) = 0,\]

and a periodic heat source,

\[h(x,y) = \sin(\pi x) \sin(2\pi y).\]

Under these conditions, the problem has an analytical solution of the form

\[u(t,x,y) = \frac{1 - e^{-(k_x+4k_y)\pi^2 t}}{(k_x+4k_y)\pi^2} \sin(\pi x) sin(2\pi y).\]

Numerical method

The spatial derivatives are computed using second-order centered differences, with the data distributed over \(nx\times ny\) points on a uniform spatial grid.

The problem is set up to use spatial grid parameters \(nx=60\) and \(ny=120\), with heat conductivity parameters \(k_x=0.5\) and \(k_y=0.75\). The problem is run using scalar relative and absolute solver tolerances of \(rtol=10^{-5}\) and \(atol=10^{-10}\).

As with the 1D version, this program solves the problem with a DIRK method, that itself uses a Newton iteration and SUNLINSOL_PCG iterative linear solver through the ARKSPILS interface. However, unlike the previous example, here the PCG solver is preconditioned using a single Jacobi iteration, and uses ARKSPILS’ built-in finite-difference Jacobian-vector product routine. Additionally, this problem uses MPI and the NVECTOR_PARALLEL module for parallelization.

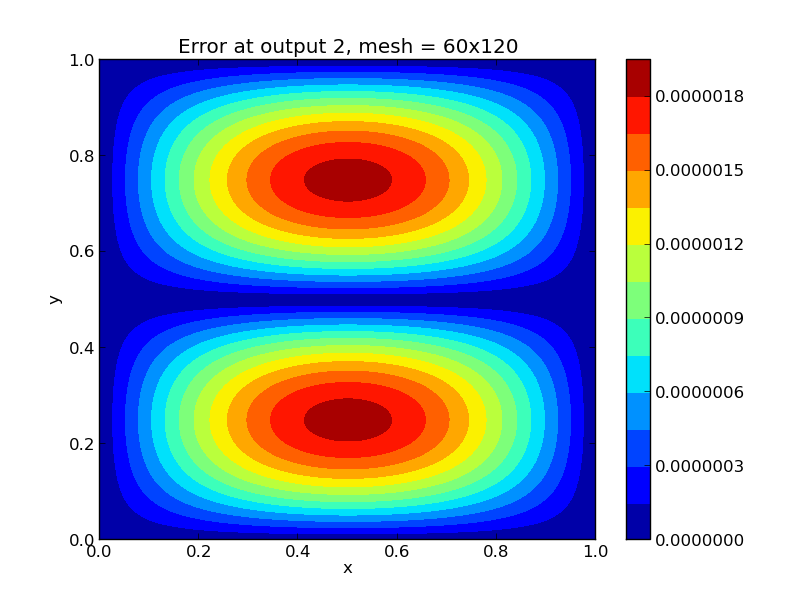
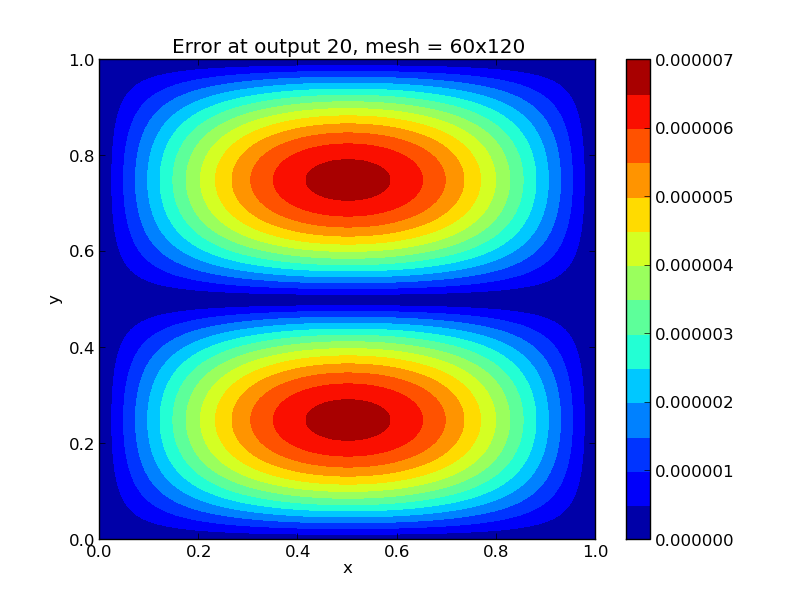
Solutions

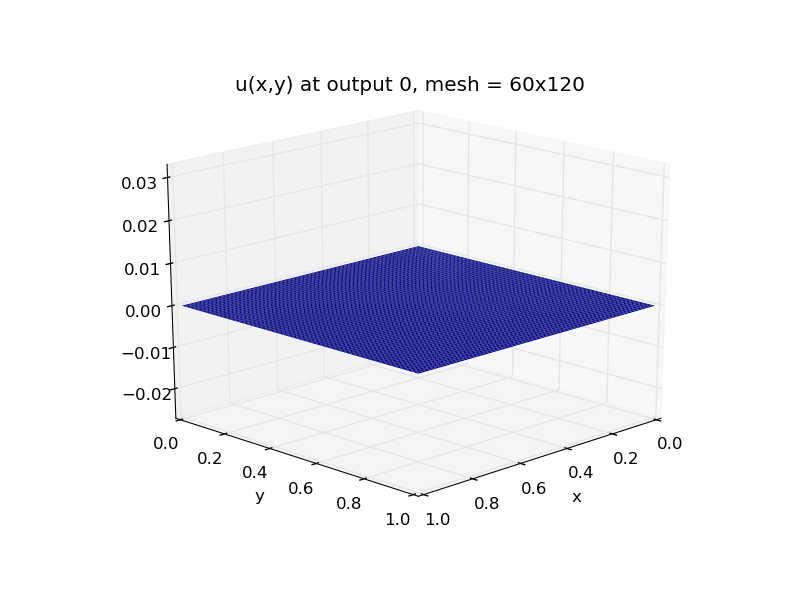
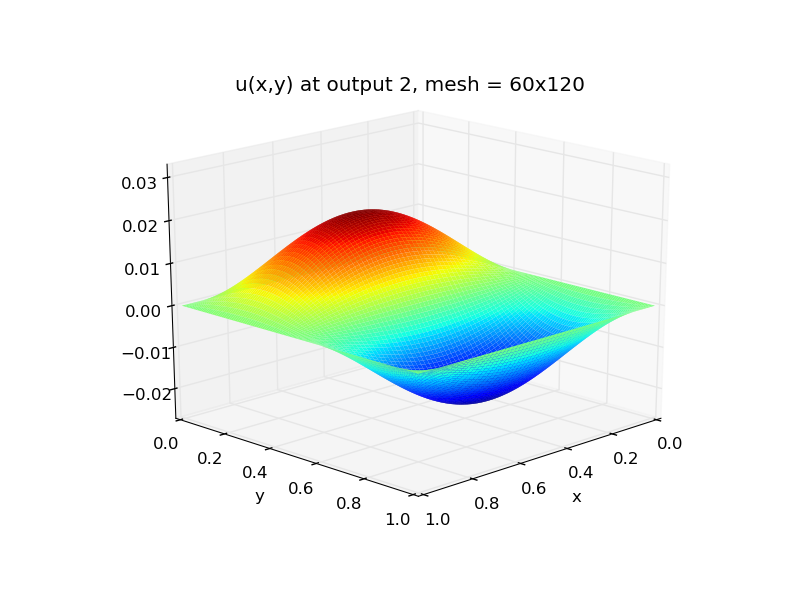
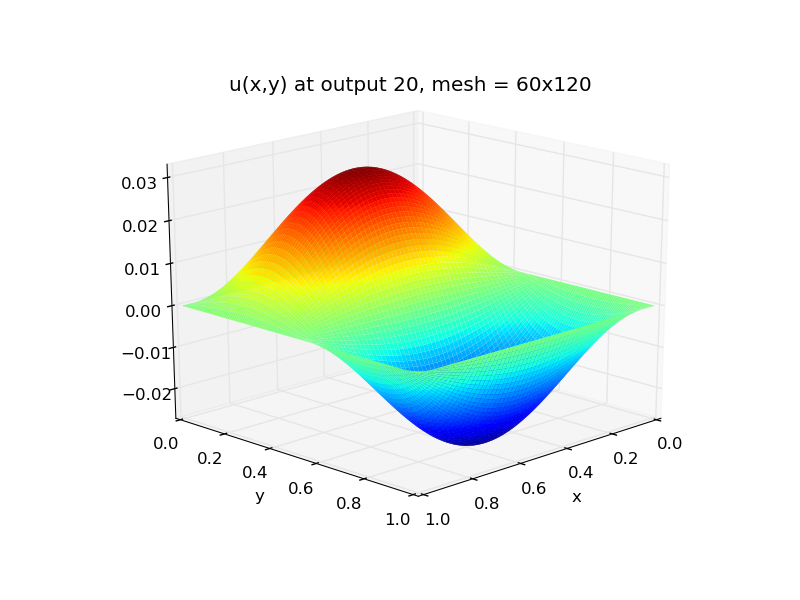
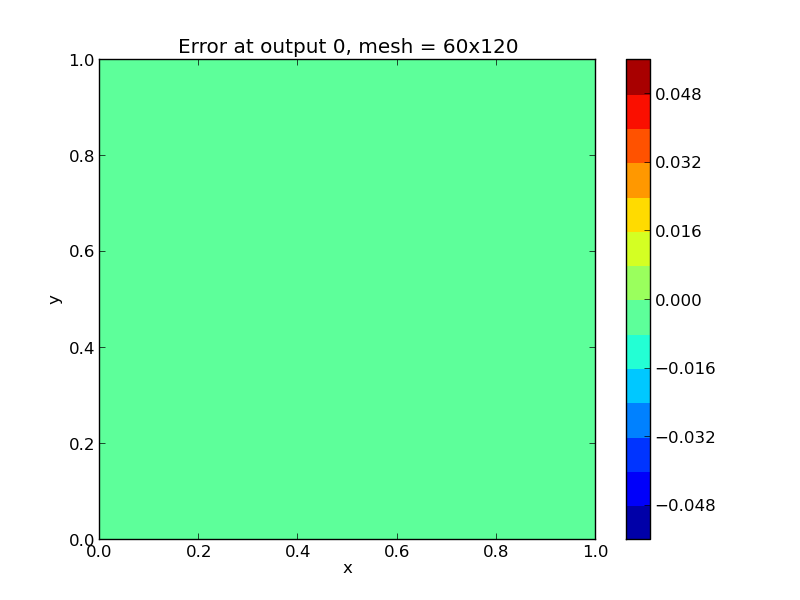
Top row: 2D heat PDE solution snapshots, the left is at time \(t=0\), center is at time \(t=0.03\), right is at time \(t=0.3\). Bottom row, absolute error in these solutions. Note that the relative error in these results is on the order \(10^{-4}\), corresponding to the spatial accuracy of the relatively coarse finite-difference mesh. All plots are created using the supplied Python script, plot_heat2D.py.